


DNA Composition, Codon Usage and Exon Prediction
Chapter published in "Genetic Databases", M.J. Bishop ed., Academic Press, 1999
Roderic Guigó
Informàtica Mèdica, Institut Municipal d'Investigació Mèdica
1
and
Departament d'Estadística, Universitat de Barcelona
February 7, 2000
In this chapter, we review the sequence based measures indicative of
protein-coding function in genomic DNA. As the genome projects
are entering the large scale sequencing phase,
computer programs are becoming essential to identify
protein coding genes in
large uncharacterized genomic sequences--typically of tens of
thousands, or even hundreds of thousands of nucleotides--
with efficiency and reliability.
At the core all gene identification programs
there exist one or more coding measures. Most such programs rely
on additional information--mainly, potential sequence signals involved
in gene specification, and sequence similarity database searches--,
and use very complex frameworks for its integration.
Still, a good knowledge of the core coding statistics is important
to understand how gene identification programs work, and to interpret
their predictions. Here we will review a few of the most important
coding measures, and we will illustrate through examples the details
involved in their computation.
1. Introduction
A coding statistic can be defined as a function that computes given a
DNA sequence a real number related to the likelihood
that the sequence is coding for a protein.
Since the early eighties, a great number of coding statistics
have been published in the literature. Most such coding statistics measure
either codon
usage bias, base compositional bias between codon positions, or periodicity
in base occurrence (or a mixture of all them).
Exhaustive reviews can be found
elsewhere (see, for instance, Gelfand gelfand:1995a
and the references therein).
Here we follow loosely the critical review by
Fickett and Tung fickett:1992a.
Our classification of coding measures is, however, slightly different.
The main distinction here
is between measures dependent of a model of coding DNA, and measures
independent of such a model. The model of coding DNA is always probabilistic,
allowing to compute the probability of a DNA sequence, given that
the sequence is coding. Although in the practice, the values (scores)
of a given coding statistic in a query sequence can be computed in a
number of different ways, here for the model-based coding statistics
we will compute scores based on such a probability. Indeed, given
a query sequence, we will compute the probability of the sequence
under the model of coding DNA, and under an alternative model or non-coding
DNA (which, here, for illustration purposes will be simply random DNA).
We will take the logarithm of the ratio of these two probabilities--the
log-likelihood ratio--as the score of the coding statistic in the
query sequence.
Model dependent coding statistics are likely to capture more of
the specific features of coding DNA--more of them
as more complex the model is (i.e. dependent on more parameters)--.
Therefore, model
dependent coding statistics may be more powerful in discriminating
coding from non-coding DNA.
Model dependent coding statistics, however, require of a representative
sample of coding DNA from the species under consideration where to estimate
the model's parameters (probabilities). The more complex the model is,
more sensible to sample bias and size. Model independent coding
statistics, on the other hand,
capture only the ``universal'' features of coding DNA; since they
do not require of a sample of coding DNA, they can be
used even in absence of previously known coding regions from the
species under consideration.
To illustrate the coding statistics reviewed here,
we will use a few test sequences.
As a genomic test sequence, we use a 2000 bp DNA sequence from the human
genome coding for the 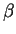 -globin gene. The sequence has been
extracted from the GenBank entry HUMHBB (EMBL entry HSHBB),
from positions 62,001 to 64,000. The human
-globin gene. The sequence has been
extracted from the GenBank entry HUMHBB (EMBL entry HSHBB),
from positions 62,001 to 64,000. The human 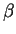 -globin gene has three
coding exons in positions 187-278, 409-631, and 1482-1610,
relative to the 2000 bp test sequence. In addition, we have
extracted two subsequences from this test sequence. The complete sequence
of the second coding exon of the
-globin gene has three
coding exons in positions 187-278, 409-631, and 1482-1610,
relative to the 2000 bp test sequence. In addition, we have
extracted two subsequences from this test sequence. The complete sequence
of the second coding exon of the 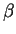 -globin gene,
which is 223 bp long, and a 223 bp long sequence
from the middle of the second intron (from positions 800 to 1022 of the
test sequence). These two sequences will serve as exonic and intronic test
sequences. We have also extracted from GenBank rel. 93 (February 1996),
a set of 450 human genes following the protocol described
in Burset and Guigó burset:1996a (see also Guigó
guigo:1997b).
From this set, exons longer than 100bp
and introns longer than 100 bp and shorter than 2500 bp were kept.
This resulted in 1753 introns and 1761 exons.
The distribution of the scores of the different coding statistics analyzed
here will be plotted in these two sets of sequences.
Results obtained in the exonic, intronic and genomic
test sequences are only for illustration purposes, and differences in
the performance of different coding statistics can not be inferred from them.
Readers interested in a rigorous comparative benchmarking should refer to
Fickett and Tung fickett:1992a.
-globin gene,
which is 223 bp long, and a 223 bp long sequence
from the middle of the second intron (from positions 800 to 1022 of the
test sequence). These two sequences will serve as exonic and intronic test
sequences. We have also extracted from GenBank rel. 93 (February 1996),
a set of 450 human genes following the protocol described
in Burset and Guigó burset:1996a (see also Guigó
guigo:1997b).
From this set, exons longer than 100bp
and introns longer than 100 bp and shorter than 2500 bp were kept.
This resulted in 1753 introns and 1761 exons.
The distribution of the scores of the different coding statistics analyzed
here will be plotted in these two sets of sequences.
Results obtained in the exonic, intronic and genomic
test sequences are only for illustration purposes, and differences in
the performance of different coding statistics can not be inferred from them.
Readers interested in a rigorous comparative benchmarking should refer to
Fickett and Tung fickett:1992a.
We will try to avoid complex mathematical formulas to describe the
algorithms, but we will indicate how to calculate them, so that
interested readers can hopefully reproduce the computations. Although,
we will thus keep mathematical formalisms to a minimum, it will be useful
to maintain a consistent notation through the chapter. Thus,
will denote a DNA sequence of length 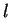 , while
, while
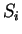 (
(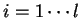 ) will denote the individual nucleotides.
For instance if
) will denote the individual nucleotides.
For instance if
then
A DNA sequence can be partitioned in a sequence of consecutive non-overlapping
codons in three different ways depending on the nucleotide in the sequence
on which the grouping of nucleotides into codons starts (that is, the
sequence can be read in three different frames). If 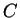 is a sequence
of codons
is a sequence
of codons
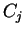 will denote the codon occupying position
will denote the codon occupying position 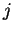 in the sequence.
If
in the sequence.
If  is a nucleotide sequence, we will use
is a nucleotide sequence, we will use 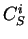 (or simply
(or simply 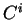 ,
,  ) to
denote the sequence of codons that results when the grouping of nucleotides
from
) to
denote the sequence of codons that results when the grouping of nucleotides
from  into codons starts at nucleotide
into codons starts at nucleotide  .
We willl use
.
We willl use 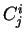 to denote the codon occupying position
to denote the codon occupying position  in
the decomposition
in
the decomposition  of the sequence.
For instance, if
of the sequence.
For instance, if  is the sequence above, then
is the sequence above, then
On the other hand, if 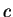 is a codon, we will use
is a codon, we will use ![$c[k]$](img24.gif) to denote the
nucleotide occupying position
to denote the
nucleotide occupying position 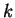 in the codon. For instance, in
the example above
in the codon. For instance, in
the example above
All the measures dependent on a probabilistic model of coding DNA
can be computed in a uniform way through the computation of
the probability of the sequence given the model.
That is, given a probabilistic model of what coding DNA
is--the codon usage table, for instance--, we can compute the
probability of a sequence of nucleotides  , assuming the sequence
is coding in a given frame. We will use
, assuming the sequence
is coding in a given frame. We will use
to denote the probability of the sequence of nucleotides  , given
that
, given
that  is coding in frame
is coding in frame  (
(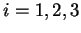 ).
On the other hand, we can compute the probability of
).
On the other hand, we can compute the probability of  given a
model of non-coding DNA. We will use
given a
model of non-coding DNA. We will use
to denote such a probability.
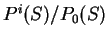 is a likelihood ratio:
the ratio of the probability of finding
the sequence of nucleotides
is a likelihood ratio:
the ratio of the probability of finding
the sequence of nucleotides  , if
, if  is coding in frame
is coding in frame  over the probability of
finding the sequence of nucleotides
over the probability of
finding the sequence of nucleotides  , if
, if  is non-coding.
To measure the coding potential of sequence
is non-coding.
To measure the coding potential of sequence  in frame
in frame  given
the model of coding DNA, we will compute the natural
logarithm of this ratio--the log-likelihood ratio,
given
the model of coding DNA, we will compute the natural
logarithm of this ratio--the log-likelihood ratio,
If 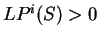 , then the probability of the
sequence of nucleotides
, then the probability of the
sequence of nucleotides  is higher assuming that
is higher assuming that  is coding in
frame
is coding in
frame  , than assuming that
, than assuming that  is non-coding in frame
is non-coding in frame  ,
while if
,
while if 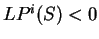 , then the probability of
, then the probability of
 is higher assuming that
is higher assuming that  does not code in frame
does not code in frame  than
assuming that
than
assuming that  is coding in frame
is coding in frame  .
Given a sequence problem
.
Given a sequence problem  , we compute the
log-likelihood ratios for
, we compute the
log-likelihood ratios for  in the three frames. If the sequence
is coding, the log-likelihood ratio will larger for one of the frames
than for the other two.
in the three frames. If the sequence
is coding, the log-likelihood ratio will larger for one of the frames
than for the other two.
Through the chapter, we will assume non-coding DNA to be simply
random DNA with nucleotide equiprobability and independence between
positions.
It could be argued that a model inferred from actual
non-coding regions of the
species under consideration should be used, instead.
However, non-coding DNA is usually underrepresented in public databases,
and it may
exhibit a high degree of heterogeneity along the genome. Therefore, we
believe that, at least for illustration purposes,
the random assumption does not introduce a significant distortion.
2.1 Measures based on oligonucleotide counts
Unequal usage of codons in the coding regions appears to be a universal
feature of the genomes across the phylogenetic spectra. This bias
obeys mainly to (i) the uneven
usage of the amino acids in the existing proteins and (ii) the uneven usage
of synonymous codons [Grantham et al.1980].
The bias in the usage of the synonymous codons correlates with the
abundance of the corresponding tRNAs [Ikemura1985].
The correlation is
particularly strong for highly expressed genes.
Codon usage is specific of the
taxonomic group, and there exist correlation between taxonomic divergence and
similarity of codon usage [Ikemura1985].
2.1.1 Codon Usage.
By comparing the frequency of codons in a region of an species genome
read in a given frame
with the typical frequency of codons in the species genes,
it is possible to estimate a likelihood of the region coding for a protein
in such a frame. Regions in which
codons are used with frequencies similar to the typical species
codon frequencies are likely to code for genes. This idea was first
introduced by Staden and McLahlan staden:1982a.
In the practice, the likelihood
can be computed in a number of different ways.
Here we compute it as a log-likelihood ratio. Let 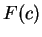 be the frequency (probability) of codon
be the frequency (probability) of codon 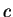 in the genes of the species
under consideration (in other words,
in the genes of the species
under consideration (in other words, 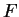 is the codon usage table,
see Table 1).
Then, given a sequence of codons
is the codon usage table,
see Table 1).
Then, given a sequence of codons
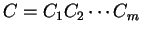 ,
and assuming independence between adjacent codons
,
and assuming independence between adjacent codons
is the probability of finding the
sequence of codons  knowing that
knowing that 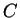 codes for a protein.
For instance, if
codes for a protein.
For instance, if  is the sequence
S= AGGACG,
when read in frame 1, it results in the sequence
is the sequence
S= AGGACG,
when read in frame 1, it results in the sequence
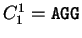 ,
,
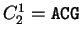 . Then
. Then
Substituting the appropriate values from Table 1,
we obtain
On the other hand, let 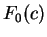 be the frequency of
codon
be the frequency of
codon 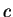 in a non-coding sequence.
in a non-coding sequence.
is the probability of
finding the sequence  if
if 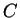 is non-coding.
Assuming the random model of coding DNA,
is non-coding.
Assuming the random model of coding DNA,
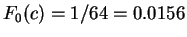 for all codons, and
for all codons, and 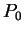 for the above sequence of codons
for the above sequence of codons 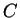 would be
would be
The log-likelihood ratio for  coding in frame
coding in frame 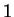 ,
, 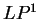 ,
is
,
is
The log-likelihood ratios for  coding in frames
coding in frames 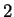 , and
, and 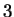 (
(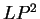 and
and 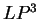 ) are computed in a similar way.
Table 4 shows the values of the log-likelihood
ratios computed on
our test exon and intron sequences, using the values of
) are computed in a similar way.
Table 4 shows the values of the log-likelihood
ratios computed on
our test exon and intron sequences, using the values of 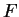 from
Table 1. As it can be seen, in this case
the log-likelihood ratio
from
Table 1. As it can be seen, in this case
the log-likelihood ratio 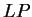 is indeed greater than zero in the
coding frame of the exon sequence, while is smaller than zero in
the non-coding frames of the exon sequence and in all frames of the intron
sequence.
is indeed greater than zero in the
coding frame of the exon sequence, while is smaller than zero in
the non-coding frames of the exon sequence and in all frames of the intron
sequence.
The distribution of the scores of the Codon Usage log-likelihood ratios
in the larger sets of intron and exon
sequences are shown in Figure 2. Because the sequences
in these sets are of very different lengths, the
scores are divided by the sequence length in order to derive these
distributions. As it is possible
to see, although the distributions are clearly distinct, there is substantial
overlap between the Codon Usage scores in the sets of intron and exon
sequences. As we will see, this is a general situation for all coding
statistics.
In the practice, the problem is not usually to determine the
likelihood that a given sequence is coding or not, but to locate the
(usually small) coding regions within large genomic sequences.
The typical procedure is to compute the value of a coding
statistic in successive (usually overlapping) windows (an sliding window),
and record the
value of the statistic for each of the windows. This generates a profile
along the sequence in which peaks may point to the coding regions and valleys
to the non-coding ones. In Figure 1,
we plot the result of sliding a window
of length 120 bp, the distance between consecutive windows being 10 bp,
computing 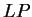 in the three different frames,
and plotting the highest value obtained. In this case, the resulting
profile reproduces fairly well the exonic structure of the human
in the three different frames,
and plotting the highest value obtained. In this case, the resulting
profile reproduces fairly well the exonic structure of the human
 -globin gene.
-globin gene.
Table 1:
The human codon usage and codon preference table as published in
http://bioinformatics.weizmann.ac.il/databases/codon. For each
codon, the table displays the frequency of usage of each codon (per thousand)
in human coding regions (first column) and the relative frequency of each
codon among synonymous codons (second column).
| The Human Codon Usage Table |
|
Gly |
GGG |
17.08 |
0.23 |
Arg |
AGG |
12.09 |
0.22 |
Trp |
TGG |
14.74 |
1.00 |
Arg |
CGG |
10.40 |
0.19 |
|
Gly |
GGA |
19.31 |
0.26 |
Arg |
AGA |
11.73 |
0.21 |
End |
TGA |
2.64 |
0.61 |
Arg |
CGA |
5.63 |
0.10 |
|
Gly |
GGT |
13.66 |
0.18 |
Ser |
AGT |
10.18 |
0.14 |
Cys |
TGT |
9.99 |
0.42 |
Arg |
CGT |
5.16 |
0.09 |
|
Gly |
GGC |
24.94 |
0.33 |
Ser |
AGC |
18.54 |
0.25 |
Cys |
TGC |
13.86 |
0.58 |
Arg |
CGC |
10.82 |
0.19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Glu |
GAG |
38.82 |
0.59 |
Lys |
AAG |
33.79 |
0.60 |
End |
TAG |
0.73 |
0.17 |
Gln |
CAG |
32.95 |
0.73 |
|
Glu |
GAA |
27.51 |
0.41 |
Lys |
AAA |
22.32 |
0.40 |
End |
TAA |
0.95 |
0.22 |
Gln |
CAA |
11.94 |
0.27 |
|
Asp |
GAT |
21.45 |
0.44 |
Asn |
AAT |
16.43 |
0.44 |
Tyr |
TAT |
11.80 |
0.42 |
His |
CAT |
9.56 |
0.41 |
|
Asp |
GAC |
27.06 |
0.56 |
Asn |
AAC |
21.30 |
0.56 |
Tyr |
TAC |
16.48 |
0.58 |
His |
CAC |
14.00 |
0.59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Val |
GTG |
28.60 |
0.48 |
Met |
ATG |
21.86 |
1.00 |
Leu |
TTG |
11.43 |
0.12 |
Leu |
CTG |
39.93 |
0.43 |
|
Val |
GTA |
6.09 |
0.10 |
Ile |
ATA |
6.05 |
0.14 |
Leu |
TTA |
5.55 |
0.06 |
Leu |
CTA |
6.42 |
0.07 |
|
Val |
GTT |
10.30 |
0.17 |
Ile |
ATT |
15.03 |
0.35 |
Phe |
TTT |
15.36 |
0.43 |
Leu |
CTT |
11.24 |
0.12 |
|
Val |
GTC |
15.01 |
0.25 |
Ile |
ATC |
22.47 |
0.52 |
Phe |
TTC |
20.72 |
0.57 |
Leu |
CTC |
19.14 |
0.20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ala |
GCG |
7.27 |
0.10 |
Thr |
ACG |
6.80 |
0.12 |
Ser |
TCG |
4.38 |
0.06 |
Pro |
CCG |
7.02 |
0.11 |
|
Ala |
GCA |
15.50 |
0.22 |
Thr |
ACA |
15.04 |
0.27 |
Ser |
TCA |
10.96 |
0.15 |
Pro |
CCA |
17.11 |
0.27 |
|
Ala |
GCT |
20.23 |
0.28 |
Thr |
ACT |
13.24 |
0.23 |
Ser |
TCT |
13.51 |
0.18 |
Pro |
CCT |
18.03 |
0.29 |
|
Ala |
GCC |
28.43 |
0.40 |
Thr |
ACC |
21.52 |
0.38 |
Ser |
TCC |
17.37 |
0.23 |
Pro |
CCC |
20.51 |
0.33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As we have pointed out, codon usage bias is a mixture of
both: bias in the usage of amino acids, and bias in the usage of
synonymous codons. Methods can be used to measure these effects separately
McCaldon and Argos mccaldon:1988a compute the probabilities
of occurrence of
different oligopeptides in existing proteins. By translating a sequence
of codons to a sequence of amino acids, the probability of the
resulting sequence of oligopeptides assuming the region to be coding
can be computed. Here, following Fickett and Tung fickett:1992a,
we compute
a measure of amino acid bias based on the observed frequencies of
single amino acids in the existing proteins. The measure is identical
to the log-likelihood ratio introduced to measure codon usage bias,
but the probability of each codon is now the observed probability of the
amino acid encoded by the codon. That is, 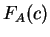 is the observed probability of the amino acid encoded by codon
is the observed probability of the amino acid encoded by codon 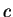 in the
existing proteins; This value can be directly derived from
a codon usage table by summing up
the probabilities of synonymous codons; that is, given a codon
in the
existing proteins; This value can be directly derived from
a codon usage table by summing up
the probabilities of synonymous codons; that is, given a codon 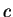
where, 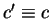 means
means 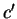 synonymous to
synonymous to 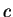 . Then,
. Then,
is the probability of finding the
sequence of amino acids resulting of translating the sequence  in frame
in frame
 given that
given that  is coding in frame
is coding in frame  .
As a model of non-coding DNA,
we assume the probability of each amino acid to be proportional to the
number of synonymous codons coding for the amino acid, that is
.
As a model of non-coding DNA,
we assume the probability of each amino acid to be proportional to the
number of synonymous codons coding for the amino acid, that is
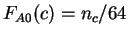 , where
, where 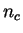 is the number of codons
synonymous to
is the number of codons
synonymous to 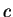 , and we can compute
, and we can compute 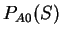 .
Then, from
.
Then, from 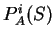 and
and 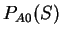 , we
compute the Amino Acid Usage log-likelihood ratio as usual.
Results obtained using this measure in our test sequences are shown in
Table 4, and Figures 1
and 2
, we
compute the Amino Acid Usage log-likelihood ratio as usual.
Results obtained using this measure in our test sequences are shown in
Table 4, and Figures 1
and 2
Gribskov et al. gribskov:1984a introduce a coding statistic to
measure uneven usage of synonymous codons solely.
Indeed, from a codon usage table, we can compute
the relative probability of each synonymous codon to code for
a given amino acid. For instance, from Table 1, we
can see that codons GAG and GAA--the two codons coding
for Glutamic Acid--are used in coding regions with probabilities
0.03882 and 0.02751 respectively, which results in a relative probability of
0.59 and 0.41, respectively. Let 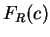 be the relative probability
in coding regions of codon
be the relative probability
in coding regions of codon 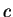 among codons synonymous to
among codons synonymous to 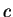 ,
,
Then
is the probability
of the sequence  given the particular sequence of amino acids coded by
given the particular sequence of amino acids coded by
 in frame
in frame  (that is, in
(that is, in 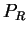 the effects of unequal usage of amino acids have been
eliminated.) We will assume that in non-coding DNA, there is
no preference between synonymous codons to code for a given amino acid.
Therefore the probability of codon
the effects of unequal usage of amino acids have been
eliminated.) We will assume that in non-coding DNA, there is
no preference between synonymous codons to code for a given amino acid.
Therefore the probability of codon 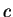 in non-coding DNA is
in non-coding DNA is
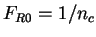 . From
. From 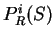 and
and 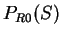 we compute the Codon Preference log-likelihood ratio as usual.
Results obtained using this measure in our test sequences are
shown in Table 4, and Figures 1 and
2.
we compute the Codon Preference log-likelihood ratio as usual.
Results obtained using this measure in our test sequences are
shown in Table 4, and Figures 1 and
2.
As it can be seen from Table 4 and Figure
1, although amino acid usage and codon
preference carry a lot of information about coding function,
neither of these measures appears to be as discriminant as codon usage.
In fact, it is easy to see that, as we have introduced them, codon
usage is the composition of amino acid usage and codon preference.
Indeed, from the definitions above, it follows directly that for a
given codon:
which results in
for a sequence  in frame
in frame  , which in turn leads to
, which in turn leads to
which states that Codon Usage bias is the sum of Amino Acid usage bias
and Codon Preference.
Bias in the distribution of oligonucleotides
other than codons (tri-nucleotides) can also be used to discriminate
between coding and non-coding regions. Bias in the usage of hexamers
may be the most discriminant one (probably because of dependence between
adjacent amino acids in the proteins).
Claverie et al. claverie:1994a were the first
to use hexamer frequencies to locate coding regions. Bias in hexamer
usage can be computed exactly as bias in codon usage. An hexamer usage
table, 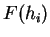 (
(
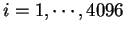 ) from the species under consideration
is computed ``a priori''. Then, the probability of a sequence of
hexanucleotides,
) from the species under consideration
is computed ``a priori''. Then, the probability of a sequence of
hexanucleotides,
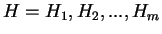 ,
in the coding frame of a coding sequence is
,
in the coding frame of a coding sequence is
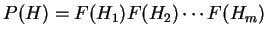 .
If
.
If 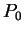 is the background probability distribution,
the log-likelihood ratio
is the background probability distribution,
the log-likelihood ratio 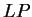 can be
computed as before. Now, a test sequence can be decomposed in
six different sequences of hexamers, instead of three,
and, thus, six log-likelihood rations
can be computed (
can be
computed as before. Now, a test sequence can be decomposed in
six different sequences of hexamers, instead of three,
and, thus, six log-likelihood rations
can be computed (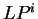 ,
, 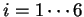 ).
Table 4 shows
the values of these ratios in our test intron and exon sequences,
Figure 2 shows the distributions of the standardized
scores (by the sequence length) in the larger sets of intron and exon
sequences, and Figure 1
shows the results of sliding a window,
and plotting the maximum of the six values at each position.
).
Table 4 shows
the values of these ratios in our test intron and exon sequences,
Figure 2 shows the distributions of the standardized
scores (by the sequence length) in the larger sets of intron and exon
sequences, and Figure 1
shows the results of sliding a window,
and plotting the maximum of the six values at each position.
Table 2:
Frequency of the four different nucleotides at the three
different codon positions in human coding regions. Derived from
Table 1
| nucleotide |
codon position |
| |
1 |
2 |
3 |
| A |
0.27 |
0.31 |
0.18 |
| C |
0.24 |
0.24 |
0.31 |
| G |
0.32 |
0.20 |
0.29 |
| T |
0.17 |
0.26 |
0.22 |
|
2.2 Measures based on base compositional bias between codon positions
From the codon usage table (Table 1), we can derive the
probability of each base at each codon position in coding regions (Table
2). As it is possible to see, there are clear
differences in the frequency with which the different bases appear at the
different codon positions; for instance, G is almost twice as frequent
as T in the first codon position, while T is more frequent than
G in the
second codon position. Similarly, C is almost twice as frequent as
A in
the third codon position, but A is more frequent than C
in the second codon position.
Sheperd shepherd:1981a already noted that
the most frequent codons were of the form RNY ( R = A or G, Y = C or T, N any nucleotide).
He suggested a method to test for the existence and frame of a coding
region by measuring the number of differences between the
sequence and the pattern
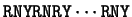 .
A number of other measures have been latter
proposed to exploit the
asymmetry in the base composition between codon positions in order to locate
potential coding regions in genomic DNA.
.
A number of other measures have been latter
proposed to exploit the
asymmetry in the base composition between codon positions in order to locate
potential coding regions in genomic DNA.
Before discussing some of these measures, we would like to point out that
asymmetry in the base composition between codon positions arises, not only
because of uneven usage of amino acids and synonymous codons, but also
because of the particular structure of the genetic code. Indeed, uneven
usage of amino acids and uneven usage of synonymous codons are not
enough to produce asymmetry in base composition, as the following example
illustrates:

Because of the structure of the genetic code, synonymous codons almost
always share the first two nucleotides (the exception
being obviously the amino acids coded by six codons, Arginine, Serine,
and Leucine). This implies that the first two positions in the codons
will be more abundant in those nucleotides common to the synonymous codons
corresponding to the most abundant amino acids. On the other hand,
differences between synonymous codons are mostly confined to the
third codon position. At this position, C and G are usually preferred, as
genes (at least, in higher eukariotes) tend to occur in G+C rich regions
(references...)
The distribution of base frequencies at codon positions
(Table 2)
can be assumed to describe statistically
a prototypical codon. Then, given a sequence problem  , we can measure
how similar to the prototypical distribution
is the observed distribution of base frequencies at the three codon
positions in
, we can measure
how similar to the prototypical distribution
is the observed distribution of base frequencies at the three codon
positions in  .
Closer the distributions,
more likely for
.
Closer the distributions,
more likely for  to be coding. As usual, there are a number of ways
in which such a ``proximity'' can be measured
[Fickett and Tung1992,Mural et al.1991].
Here we will compute the usual log-likelihood ratio.
to be coding. As usual, there are a number of ways
in which such a ``proximity'' can be measured
[Fickett and Tung1992,Mural et al.1991].
Here we will compute the usual log-likelihood ratio.
Let 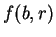 be the probability of nucleotide
be the probability of nucleotide 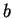 at codon position
at codon position 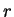 , as
estimated from known coding regions (Table 2). Then,
if
, as
estimated from known coding regions (Table 2). Then,
if 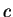 is a codon
is a codon
is the probability of codon 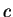 in coding regions, assuming independence
between adjacent nucleotides. On the other hand,
we will assume
in coding regions, assuming independence
between adjacent nucleotides. On the other hand,
we will assume 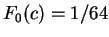 the probability of
for all triplets
the probability of
for all triplets 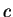 in non-coding DNA. From
in non-coding DNA. From 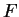 and
and 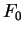 ,
, 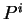 and
and 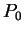 can be computed exactly as done before
in deriving the codon usage log-likelihood ratio.
For instance, if the sequence
can be computed exactly as done before
in deriving the codon usage log-likelihood ratio.
For instance, if the sequence  is AGGACG,
the probability of
is AGGACG,
the probability of  , if
, if  is coding in frame 1, can be computed as
is coding in frame 1, can be computed as
From Table 2, we obtain
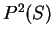 and
and 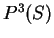 are computed in a similar way.
From
are computed in a similar way.
From 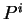 , and
, and 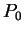 , the Codon Preference log-likelihood ratio
is derived as usual.
Results obtained using this measure are shown in
Table 4, and Figures 1 and
2.
, the Codon Preference log-likelihood ratio
is derived as usual.
Results obtained using this measure are shown in
Table 4, and Figures 1 and
2.
Both Codon Prototype and Codon Usage are based on a model of coding
DNA described by the probabilities of the codons. The models, however,
are very different. In Codon Usage, the model is described by the explicit
probability of each codon. In Codon Prototype, the model is simply
described by the probability of occurrence of each base at each position
in a codon. Codon Prototype and
Codon Usage would be equivalent if codon positions were independent.
This is not clearly the case: frequencies of codons derived
from Table 2 assuming independence between
codon positions are substantially different than the observed
codon frequencies (Table 1). Measures based on
the frequency of usage of oligonucleotides, such as Codon Usage,
implicitly capture such dependences between nucleotide positions
within codons in coding regions. Dependencies between nucleotide positions
in coding regions, however, can be explicitly described by means of
Markov Models.
Borodovsky and McIninch borodovsky:1993a first introduced
the usage of Markov Models
to locate potential coding regions in DNA sequences. For illustration
purposes, it may be helpful to introduce Markov Models from Codon Prototype.
As we have seen, in Codon Prototype, the probability of a nucleotide
to appear in a given codon position is constant,
independent of the nucleotides in nearby positions.
For instance, if  is the sequence above (
is the sequence above (
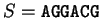 ),
the probability of G at codon position 3 (
),
the probability of G at codon position 3 (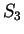 and
and 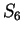 )
is constant, 0.29, whether the nucleotide
preceding G is G (as in
)
is constant, 0.29, whether the nucleotide
preceding G is G (as in 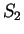 ) or C (as in
) or C (as in 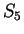 ).
In the Markov Models, however, the probability of a nucleotide at
a particular codon position depends (is conditionated)
on the nucleotide(s) preceding it.
).
In the Markov Models, however, the probability of a nucleotide at
a particular codon position depends (is conditionated)
on the nucleotide(s) preceding it.
In the simplest of the Markov Models, the Markov Models of order 1,
the probability of a nucleotide depends only on the preceding nucleotide.
In this case, the model of coding DNA is based on the probabilities
of the four nucleotides at each codon position, depending on the
nucleotide occurring at the preceding codon position (technically called
the transition probabilities). Thus, instead of
one single matrix, as in Codon Prototype, three 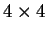 matrices (the transition matrices) are required,
matrices (the transition matrices) are required,
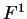 ,
, 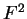 , and
, and 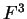 , each one corresponding to a different codon position.
Coefficient
, each one corresponding to a different codon position.
Coefficient 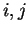 from matrix
from matrix 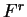 ,
, 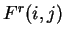 ,
corresponds to the probability of
nucleotide
,
corresponds to the probability of
nucleotide  in codon position
in codon position 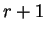 (position
(position 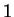 , if
, if 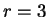 ), given that
nucleotide
), given that
nucleotide 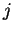 is at codon position
is at codon position 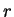 . We have estimated these matrices
from the sample of 1761 human exons.
The conditional probability of nucleotides
. We have estimated these matrices
from the sample of 1761 human exons.
The conditional probability of nucleotides
 in codon position
in codon position 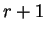 , given nucleotide
, given nucleotide 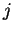 in codon position
in codon position 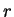 ,
is estimated by the number of times that
di-nucleotide
,
is estimated by the number of times that
di-nucleotide 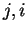 appears at codon position
appears at codon position 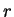 over the total number of times that
nucleotide
over the total number of times that
nucleotide 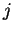 appears at codon position
appears at codon position 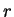 .
These matrices are shown in Table 3.
Indeed, we can see from them that
the probability of G at codon position 3, given that C is
at codon position 2, is 0.27, but the probability of G at codon
position 3 given that G is at codon position 2 is 0.37.
.
These matrices are shown in Table 3.
Indeed, we can see from them that
the probability of G at codon position 3, given that C is
at codon position 2, is 0.27, but the probability of G at codon
position 3 given that G is at codon position 2 is 0.37.
The probability of  above, given that
above, given that  is coding in frame 1,
can be computed now as
is coding in frame 1,
can be computed now as
Obviously, the probability of the first nucleotide in the sequence
is not described by the transition matrices, because it is not
preceded by any nucleotide.
As the probability of the first nucleotide in the
sequence (the initial probability) we can assume simply the
probability of such nucleotide depending on its codon position, that
is, the value in the Codon Prototype Table (Table 2).
Then, substituting the appropriate values from Tables 3 and
2 in the above equation, we obtain the probability
of  coding in frame 1:
coding in frame 1:
Similarly, the probability of the sequence of nucleotides  , given that
, given that
 codes in frame 2 is
codes in frame 2 is
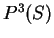 can be computed in exactly the same way.
If
can be computed in exactly the same way.
If 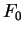 is the matrix of conditional probabilities of the different
nucleotides given the preceding ones, we can compute the usual log-likelihood
ratio. Assuming a random model of non-coding DNA, the probability of
a nucleotide
is the matrix of conditional probabilities of the different
nucleotides given the preceding ones, we can compute the usual log-likelihood
ratio. Assuming a random model of non-coding DNA, the probability of
a nucleotide  does not depend on the preceding nucleotide
does not depend on the preceding nucleotide
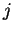 , then
, then
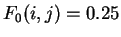 for each pairs of nucleotides
for each pairs of nucleotides 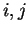 ,
Results obtained in the test sequences
with the log-likelihood ratios corresponding to
a Markov Model of order 1 are shown in
Table 4, and Figures 1 and
2.
,
Results obtained in the test sequences
with the log-likelihood ratios corresponding to
a Markov Model of order 1 are shown in
Table 4, and Figures 1 and
2.
Table 3:
Probabilities of the four nucleotides at the different codon positions
conditioned to the nucleotide in the preceding codon position.
Estimated from our set of human exon and intron sequences.
| |
|
codon position 1 |
| |
|
A |
C |
G |
T |
| |
A |
.36 |
.27 |
.35 |
.18 |
| |
C |
.21 |
.23 |
.24 |
.27 |
| |
G |
.19 |
.14 |
.23 |
.23 |
| |
T |
.24 |
.35 |
.19 |
.31 |
|
|
|
|
|
|
|
| |
|
codon position 2 |
| |
|
A |
C |
G |
T |
| |
A |
.16 |
.19 |
.15 |
.07 |
| |
C |
.28 |
.44 |
.41 |
.33 |
| |
G |
.40 |
.12 |
.27 |
.45 |
| |
T |
.16 |
.25 |
.17 |
.16 |
|
|
|
|
|
|
|
| |
|
codon position 3 |
| |
|
A |
C |
G |
T |
| |
A |
.22 |
.33 |
.24 |
.13 |
| |
C |
.21 |
.29 |
.27 |
.21 |
| |
G |
.44 |
.15 |
.37 |
.53 |
| |
T |
.13 |
.22 |
.12 |
.13 |
|
|
|
|
|
|
|
|
In Markov Models of order 2, the probability of
a given nucleotide at a given codon position
depends on the di-nucleotide preceding it. The transition matrices have now
4 raws and 16 columns (one for each possible di-nucleotide).
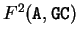 , for instance, would be the probability of A
following the di-nucleotide GC at codon position 2 (that is, A
would be at codon position 1).
In general, the order of the Markov Model indicates the number of
preceding nucleotides on which the probability of a given nucleotide depends.
In a Markov Model of order
, for instance, would be the probability of A
following the di-nucleotide GC at codon position 2 (that is, A
would be at codon position 1).
In general, the order of the Markov Model indicates the number of
preceding nucleotides on which the probability of a given nucleotide depends.
In a Markov Model of order 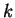 , thus, the coefficients
, thus, the coefficients 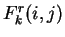 correspond to the probability of oligonucleotide
correspond to the probability of oligonucleotide 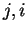 of length
of length 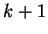 at codon position
at codon position 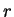 , given oligonucleotide
, given oligonucleotide  of length
of length 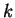 at codon
position
at codon
position 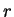 . These probabilities are estimated by the frequency of
oligonucleotide
. These probabilities are estimated by the frequency of
oligonucleotide 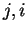 of length
of length 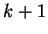 at codon position
at codon position 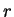 over the frequency of oligonucleotide
over the frequency of oligonucleotide 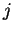 of length
of length
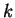 at position
at position 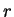 .
Borodovsky and McIninch borodovsky:1993a investigate Markov Models
of order up to
.
Borodovsky and McIninch borodovsky:1993a investigate Markov Models
of order up to 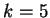 .
Results obtained in the test sequences with
Markov Models of order 2 and 5 are shown in
Table 4, and Figures 1 and
2.
.
Results obtained in the test sequences with
Markov Models of order 2 and 5 are shown in
Table 4, and Figures 1 and
2.
Markov Models of higher order may capture more of the intrinsic features
of coding DNA, but on the other hand they also depend on more parameters.
Since Markov Models of order 2 are based on counts of tri-nucleotides
they are, somehow, similar to Codon Usage. However, while Codon Usage
reflects only dependences between contiguous nucleotides
within codons, a Markov Model of order 2 also reflects
nucleotide dependences between nucleotides in
contiguous codons. Consequently, it also
depends on more parameters: while Codon Usage depends on 64 probabilities,
a Markov Model of order 2 depends on four 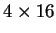 matrices (corresponding
to the three transition matrices and the initial probabilities matrix),
that is, it depends on 256 estimated probabilities.
A similar reasoning can be applied to the relationships between Hexamer
Usage and Markov Models of order
matrices (corresponding
to the three transition matrices and the initial probabilities matrix),
that is, it depends on 256 estimated probabilities.
A similar reasoning can be applied to the relationships between Hexamer
Usage and Markov Models of order 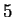 .
.
Figure 1:
Values of the model based Coding Statistics along the
2000 bp human 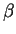 -globin gene sequence,
computed on an sliding window of length 120 and step 10.
-globin gene sequence,
computed on an sliding window of length 120 and step 10.
|
truein
truein
|
Figure 2:
Distribution of the scores of the model based Coding Statistics
in the set of 1761 human exons and 1753 human intron sequences.
To plot them, the values
of the Coding Statistics are divided by the length of the sequence.
|
truein
truein
|
All the methods reviewed so far
rely on a probabilistic model of what coding DNA is, under which the coding
likelihood of DNA sequences is computed.
To estimate the probabilities describing the coding
model (of codons, amino acids,
synonymous codons, hexamers, nucleotides at codon positions, ...)
an non-biased sample of coding DNA is ideally required. However, for most
species
such a sample does not exist. Indeed for most eukariotic organisms
(other than Sacharomices cerevisiae and
maybe Caenorhabditis elegans)
only an small fraction of the genes are known, and the set of known genes
tend to be biased towards the highly expressed ones--which are likely
to exhibit characteristic sequence features as, for instance, strong
codon preference bias--. The situation is even worst in the case of
the prokariotic genomes. Recent technological progress has made shotgun
sequencing of whole prokariotic genomes (up to a few megabases) feasible.
It is usually the case, thus, that no sequences of genes are known before the
whole genome a prokariotic organism is sequenced.
Coding measures
not depending of an ``a priori'' model of coding DNA would, therefore,
be very useful. A number of such measures have been proposed.
In general, the underlying assumption
is that coding DNA is less ``random'' or ``homogeneous'' than non coding DNA
with respect to some feature related to codigness--codon usage, base
composition--. Deviation from randomness or inhomogeneity can be measured
independently of a reference model, and the resulting score
correlated with coding function. Since there is no reference model,
these scores do not have a direct probabilistic meaning, although their
distribution can be empirically studied in known sets of coding and
non-coding sequences.
Obviously, deviation from randomness or inhomogeneity may in the practice
mean a number of different things. Fichant and Gautier fichant:1987a,
for instance, measure, using Correspondence Analysis,
the degree of homogeneity in codon usage between the three frames
of the sequence problem. The assumption is that if the sequence is coding,
codon usage will be markedly different in the coding frame than in the
two other frames--and therefore it will exist inhomogeneity in codon
usage between frames--, while if the sequence is not coding, codon usage will
be the essentially the same in the three frames--and codon usage will be
homogeneous between frames. While
Fichant and Gautier fichant:1987a measure is
based on the usage of codons, Fickett and Tung fickett:1982a and
Staden staden:1984a propose
measures independent of a reference model, based on the asymmetry in
the base composition between codon positions. We discuss one such measure
next.
The goal here is to measure how asymmetric is
the distribution of nucleotides at the three triplet positions
in the sequence problem. Both,
Fickett and Tung fickett:1982a and
Staden staden:1984a
calculate the asymmetry independently for each nucleotide (although using
different formulas), and then combine the values into a single score.
Staden staden:1984a simply sums the four values.
Fickett and Tung fickett:1982a,
in the widely used TESTCODE program, considers in addition the
frequencies of the four nucleotides. Each of the asymmetries
and frequencies is used to make an estimate of coding likelihood--which
makes this measure dependent of a sample set of known coding and non-coding
sequences--, and the
separate estimates are all combined using a linear weighted sum.
Here we also compute the asymmetry independently for each nucleotide,
simply as the variance of the frequency of the nucleotide at the
three codon positions as suggested in
Fickett and Tung fickett:1992a, and sum the
four values obtained into a single score.
Let 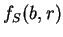 be the (relative)
frequency of nucleotide
be the (relative)
frequency of nucleotide 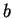 at codon position
at codon position 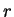 in the sequence problem
in the sequence problem  , as calculated from one of the three
decompositions of
, as calculated from one of the three
decompositions of  in codons (any of them).
Let
in codons (any of them).
Let
be the average frequency of nucleotide 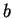 at the three codon positions,
and let's define the asymmetry in the distribution of nucleotide
at the three codon positions,
and let's define the asymmetry in the distribution of nucleotide 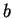 ,
as the variance of this frequency
,
as the variance of this frequency
Note that the value of asym is independent of the frame in
is independent of the frame in  in which the codons are defined.
Therefore, only one value of asymmetry needs to be computed along
the sequence problem (and not one for each frame, as we have been doing
so far).
Then we compute the Position Asymmetry of the sequence, PA(
in which the codons are defined.
Therefore, only one value of asymmetry needs to be computed along
the sequence problem (and not one for each frame, as we have been doing
so far).
Then we compute the Position Asymmetry of the sequence, PA( ) as
) as
Table 4,
and Figures 5 and 6 show the results
obtained when PA is computed in our test sequences.
Given a DNA sequence, we can compute how many times nucleotide  is
followed by nucleotide
is
followed by nucleotide 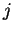 at a distance of
at a distance of 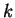 nucleotides,
nucleotides, 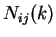 .
For instance, if the sequence
.
For instance, if the sequence
then 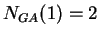 ,
, 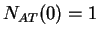 ,
, 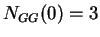 ,
, 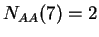 , and so on.
Figure 3 shows the absolute frequency of the pair
, and so on.
Figure 3 shows the absolute frequency of the pair
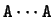 with
with 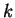 nucleotides between the two A's
occurring in the 200 first base pairs of the
sequences in our test sets of human exons and introns.
As it is possible to see, a clear periodic pattern arises from the set of
exon sequences. The nucleotide A is more likely to be found
at distance
nucleotides between the two A's
occurring in the 200 first base pairs of the
sequences in our test sets of human exons and introns.
As it is possible to see, a clear periodic pattern arises from the set of
exon sequences. The nucleotide A is more likely to be found
at distance
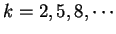 from another A than at other distances.
Note that nucleotide pairs at a distance of
from another A than at other distances.
Note that nucleotide pairs at a distance of
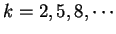 nucleotides, are at the
same codon position, whereas nucleotide pairs at other distances, are not.
Such a periodic pattern reflects correlations between nucleotide positions
along coding sequences (that is, the probability of finding a nucleotide
at a given position in a coding sequences is not independent of the
nucleotide occurring at some other--even distant--position).
The correlations arise, in turn, because of the asymmetry in base composition
at the three codon positions in coding sequences [Gutiérrez et al.1994].
The periodic pattern,
which is characteristic of the 16 pairs
of nucleotides, and not only of the pair
nucleotides, are at the
same codon position, whereas nucleotide pairs at other distances, are not.
Such a periodic pattern reflects correlations between nucleotide positions
along coding sequences (that is, the probability of finding a nucleotide
at a given position in a coding sequences is not independent of the
nucleotide occurring at some other--even distant--position).
The correlations arise, in turn, because of the asymmetry in base composition
at the three codon positions in coding sequences [Gutiérrez et al.1994].
The periodic pattern,
which is characteristic of the 16 pairs
of nucleotides, and not only of the pair
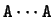 ,
is absent in the intronic sequences.
,
is absent in the intronic sequences.
A number of coding statistics have been devised based in measuring
the periodic structure (or the correlation structure) of DNA sequences.
We discuss three such measures next. Konopka konopka:1990a in
the Position Asymmetry Index, compares the probability of pairs of the
same nucleotide to appear at a distance
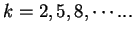 (that
is, at the same codon position) in the
query sequence with the probability of these pairs to appear at other
distances (different codon positions),
Herzel and Große herzel:1995a in the Average Mutual Information,
compare the correlations of all pairs of
nucleotides at the same codon positions with the correlations
at different codon positions. Finally, Tiwari et al.
tiwari:1997a use the relative
peak at the frequency
(that
is, at the same codon position) in the
query sequence with the probability of these pairs to appear at other
distances (different codon positions),
Herzel and Große herzel:1995a in the Average Mutual Information,
compare the correlations of all pairs of
nucleotides at the same codon positions with the correlations
at different codon positions. Finally, Tiwari et al.
tiwari:1997a use the relative
peak at the frequency 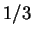 in the Fourier spectrum of the sequence.
in the Fourier spectrum of the sequence.
Figure:
Periodic structure in DNA sequences.
The absolute frequency of the pair
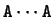 with
with 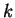 (from 0 to 5)
nucleotides between the two A's
in the 200 first base pairs of the
sequences in the set of 1761 human exons and 1753 human introns.
A clear period-3 pattern appears in coding regions, which is absent in
non-coding regions. Due to the finite size of the sequences (200 bp)
the periodic pattern vanishes at longer distances
(from 0 to 5)
nucleotides between the two A's
in the 200 first base pairs of the
sequences in the set of 1761 human exons and 1753 human introns.
A clear period-3 pattern appears in coding regions, which is absent in
non-coding regions. Due to the finite size of the sequences (200 bp)
the periodic pattern vanishes at longer distances 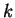 . A similar
periodic pattern appears in coding regions
for the other fifteen possible pairs of nucleotides.
. A similar
periodic pattern appears in coding regions
for the other fifteen possible pairs of nucleotides.
 |
Given a sequence  , Konopka
konopka:1990a considers three distinct probabilities,
the probability
, Konopka
konopka:1990a considers three distinct probabilities,
the probability 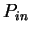 of finding pairs of the same nucleotide at distances
of finding pairs of the same nucleotide at distances
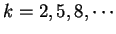 ,
the probability
,
the probability 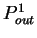 of finding pairs of the same nucleotide
at distances
of finding pairs of the same nucleotide
at distances
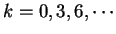 , and
the probability
, and
the probability 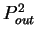 of finding pairs of the same nucleotide at
distances
of finding pairs of the same nucleotide at
distances
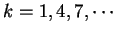 . Because of the 3-base periodic pattern,
in coding regions
. Because of the 3-base periodic pattern,
in coding regions 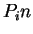 will be
larger than the other two probabilities, while in non-coding regions
the three probabilities will be similar. The tendency to cluster
homogeneous di-nucleotides in a 3-base periodic pattern can be measured by
the Periodic Asymmetry Index
will be
larger than the other two probabilities, while in non-coding regions
the three probabilities will be similar. The tendency to cluster
homogeneous di-nucleotides in a 3-base periodic pattern can be measured by
the Periodic Asymmetry Index
which can be taken as an indicative of the coding potential of the
sequence  ;
In fact, Konopka konopka:1990a computes the Periodic Asymmetry Index
in an slightly different way, he computes
the tendency to cluster
di-nucleotides in a 2-base periodic pattern (suggested to be characteristic
of intronic sequences) and computes the Periodic Asymmetry Index
as the ratio of the two tendencies (2-base over 3-base periodicity).
;
In fact, Konopka konopka:1990a computes the Periodic Asymmetry Index
in an slightly different way, he computes
the tendency to cluster
di-nucleotides in a 2-base periodic pattern (suggested to be characteristic
of intronic sequences) and computes the Periodic Asymmetry Index
as the ratio of the two tendencies (2-base over 3-base periodicity).
Table 4,
and Figures 5 and 6 show the results
obtained when PAI is computed in our test sequences.
Given a sequence  , let
, let 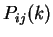 be
the probability in the sequence of the pair of nucleotides
be
the probability in the sequence of the pair of nucleotides  and
and 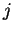 at a
distance of
at a
distance of 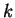 nucleotides.
These probabilities can be estimated by the absolute frequencies
nucleotides.
These probabilities can be estimated by the absolute frequencies 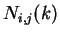 above (see Li li:1997a for considerations regarding the estimation
of these probabilities). The correlation between nucleotide
above (see Li li:1997a for considerations regarding the estimation
of these probabilities). The correlation between nucleotide  and
nucleotide
and
nucleotide 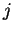 at a distance of
at a distance of 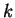 nucleotides can be calculated
[Li1997] as:
nucleotides can be calculated
[Li1997] as:
where 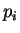 and
and 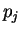 are the probabilities of nucleotides
are the probabilities of nucleotides  and
and  in
in  .
Thus, for each distance
.
Thus, for each distance 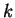 , sixteen different individual correlations can be
calculated. A measure that summarizes all individual correlations at a given
distance
, sixteen different individual correlations can be
calculated. A measure that summarizes all individual correlations at a given
distance 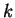 is the Mutual Information function [Shannon1948]:
is the Mutual Information function [Shannon1948]:
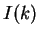 quantifies the amount of information that can be obtained from
one nucleotide about another nucleotide at a distance
quantifies the amount of information that can be obtained from
one nucleotide about another nucleotide at a distance 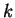 .
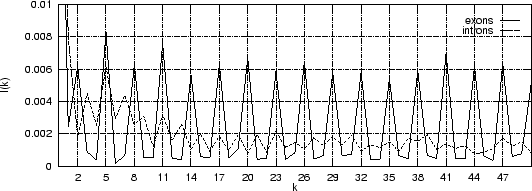
Figure 4 shows the Mutual Information Function computed on
the first 200 bp of the sequences in the set of human exons and introns.
The 3-base periodic pattern in coding sequences
becomes obvious.
.
Figure 4 shows the Mutual Information Function computed on
the first 200 bp of the sequences in the set of human exons and introns.
The 3-base periodic pattern in coding sequences
becomes obvious. 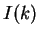 has larger values
for
has larger values
for
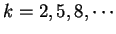 .
The pattern is absent in non-coding sequences.
.
The pattern is absent in non-coding sequences.
In coding DNA, thus, 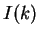 oscillates between two values, while
in non-coding DNA,
oscillates between two values, while
in non-coding DNA, 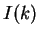 is rather flat.
Herzel and Große herzel:1995a use this fact to construct a
coding statistic.
They call the two values between which
is rather flat.
Herzel and Große herzel:1995a use this fact to construct a
coding statistic.
They call the two values between which 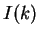 oscillates in coding DNA,
the in-frame mutual information
oscillates in coding DNA,
the in-frame mutual information 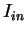 at distances
at distances
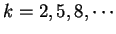 , and the out-of-frame mutual information
, and the out-of-frame mutual information
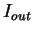 at
at
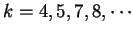 .
They show that
.
They show that
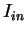 and
and 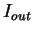 can be computed directly from the probabilities
can be computed directly from the probabilities
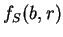 of the nucleotide
of the nucleotide 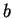 to appear at codon position
to appear at codon position
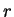 , as estimated from
, as estimated from  . In order to reduce the pair of numbers
. In order to reduce the pair of numbers
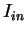 and
and 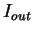 to a single quantity, they compute the
Average Mutual Information as [Gro
to a single quantity, they compute the
Average Mutual Information as [Gro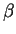 e et al.1998]
e et al.1998]
Table 4,
and Figures 5 and 6 show the results
obtained when AMI is computed in our test sequences.
Figure 4:
The Mutual Information function computed for distances from 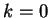 to
to 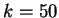 in the 200 first bp from the sequences in set of 1761 human exons
and in the set of 1753 human introns.
in the 200 first bp from the sequences in set of 1761 human exons
and in the set of 1753 human introns.
 |
Correlation structures in DNA sequences--such as those measured in AMI--
may reveal biologically relevant large scale heterogeneity in genomic
sequences, other than coding. For a review of correlation structures in
DNA sequences, and their biological implication see [Li1997].
Periodic correlations in DNA sequences can also be examined by means
of Fourier Analysis. The partial spectrum of a DNA sequence  of length
of length 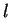 corresponding to nucleotide
corresponding to nucleotide 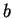 is defined
as [Li et al.1994,Silverman and Linsker1986]:
is defined
as [Li et al.1994,Silverman and Linsker1986]:
where 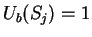 if
if 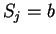 , and it is 0 otherwise, and
, and it is 0 otherwise, and
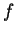 is the discrete frequency,
is the discrete frequency, 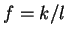 , with
, with
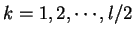 .
The total Fourier Spectrum of the DNA sequence is the sum of the
four partial Spectra:
.
The total Fourier Spectrum of the DNA sequence is the sum of the
four partial Spectra:
DNA coding regions reveal the characteristic periodicity
of 3 as a distinct peak at frequency 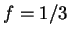 . No such ``peak'' is
apparent for non-coding sequences [Tsonis et al.1991], [Tiwari et al.1997].
We have computed the Fourier Spectrum at
. No such ``peak'' is
apparent for non-coding sequences [Tsonis et al.1991], [Tiwari et al.1997].
We have computed the Fourier Spectrum at 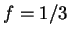 (
(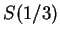 )
in our test sequences. Results appear in Table 4,
and Figures 5 and 6.
As it is possible to see from Figure 5, the
Fourier Spectrum profile in the human
)
in our test sequences. Results appear in Table 4,
and Figures 5 and 6.
As it is possible to see from Figure 5, the
Fourier Spectrum profile in the human 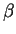 globin gene sequences
is identical (save scale) to the Position Asymmetry profile.
This indicates that there is a one to one correspondence between
Fourier Spectrum and Position Asymmetry, and that one measure can
be directly derived from the other. In fact, this can be shown analytically
(Ivo Große, personal comunication).
The relation between the
two measures depends on the length of the sequence, as the dissimilar
distributions of the Position Asymmetry and Fourier Spectrum scores
indicates in the set of 1761 human exons and 1753 human introns,
which have variable length.
globin gene sequences
is identical (save scale) to the Position Asymmetry profile.
This indicates that there is a one to one correspondence between
Fourier Spectrum and Position Asymmetry, and that one measure can
be directly derived from the other. In fact, this can be shown analytically
(Ivo Große, personal comunication).
The relation between the
two measures depends on the length of the sequence, as the dissimilar
distributions of the Position Asymmetry and Fourier Spectrum scores
indicates in the set of 1761 human exons and 1753 human introns,
which have variable length.
Actually, in order to obtain a cleaner signal, Tiwari et al.
tiwari:1997a build the ratio of the Fourier Spectrum at 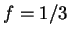 over the average of the total spectrum of the sequence,
over the average of the total spectrum of the sequence,
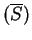 ,
which can be computed from the frequencies of the nucleotides along
the sequence.
,
which can be computed from the frequencies of the nucleotides along
the sequence.
Figure 5:
Values of the model independent
Coding Statistics along the
2000 bp human 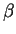 -globin gene sequence,
computed on an sliding window of length 120 and step 10.
-globin gene sequence,
computed on an sliding window of length 120 and step 10.
|
truein
|
Figure 6:
Distribution of the scores of the model independent Coding Statistics
in the set of 1761 human exons and 1753 human intron sequences.
To plot them, the values
of the Coding Statistics are divided by the length of the sequence.
|
truein
|
Table 4:
Values of different coding statistics in
the 223 bp long second coding exon of the human 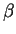 -globin gene,
and in a 223 bp long sequence from the middle of the second intron
of the same gene
-globin gene,
and in a 223 bp long sequence from the middle of the second intron
of the same gene
|
| |
|
exon sequence |
intron sequence |
| |
|
coding frame |
non coding frames |
frame 1 |
frame 2 |
frame 3 |
| Codon Usage |
24.06 |
-16.13 |
-3.16 |
-14.36 |
-23.74 |
-19.67 |
| Hexamer Usage |
27.62 |
-11.64 |
-6.51 |
-20.90 |
-27.56 |
-22.07 |
| |
|
39.98 |
-14.58 |
-8.46 |
-26.73 |
-27.81 |
-25.87 |
| Codon Preference |
15.97 |
-1.32 |
7.24 |
-7.96 |
-12.70 |
-14.93 |
| Amino Acid Usage |
8.17 |
-14.87 |
-10.17 |
-6.15 |
-10.69 |
-4.57 |
| Codon Prototype |
9.87 |
-11.23 |
-10.30 |
-11.45 |
-17.44 |
-14.49 |
| Markov Model |
order 1 |
29.92 |
-2.69 |
-3.31 |
-35.44 |
-42.40 |
-41.73 |
| |
order 2 |
34.73 |
-18.26 |
-7.77 |
-29.61 |
-41.76 |
-40.05 |
| |
order 5 |
72.69 |
-21.38 |
13.56 |
-37.63 |
-30.99 |
-36.40 |
| Position Asymmetry |
0.0957 |
0.0211 |
| Periodic Asymmetry Index |
1.159 |
1.009 |
| Average Mutual Information |
0.00681 |
0.000344 |
| Fourier Spectrum |
2.278 |
0.892 |
|
A number of gene identification programs for prediction of gene
structure in large genomic regions are currently available.
Table 5 shows a list of available programs
and Internet sites to access them. See Fickett fickett:1996a,
Guigó guigo:1997a and Claverie claverie:1997a
for recent reviews, Burset and Guigó
burset:1996a for a comparative benchmark,
and the WWW document maintained by Wential Li
at linkage.rockefeller/edu/wli/gene/list.html for an up-to-date
list of references. At the core of all such programs, there exists one
or more coding statistics related to the measures reviewed here.
Indeed, currently more powerful programs are entirely built on Hidden
Markov Models (GenScan [Burge and Karlin1997], Genie [Kulp et al.1996],
Veil [Henderson et al.1997]), which can be seen as a generalization of the
Markov Models discussed here.
Table 5:
List of Gene Identification programs, and Internet access.
e-mail server address is provided when different from the WWW address.
|
Program |
Authors |
WWW address |
|
|
GENEMODELER |
Fields and Soderlund, 1990 |
|
|
|
GENEID |
Guigó et al., 1992 |
genome.imim.es/geneid.html |
|
|
|
|
geneid@darwin.bu.edu |
|
|
SORFIND |
Hutchinson and Hayden, 1992 |
|
|
|
GENEPARSER |
Snyder and Stormo, 1993 |
beagle.colorado.edu/ eesnyder/GeneParser.html |
|
|
GENEMARK |
Borodovski and McIninch, 1993 |
intron.biology.gatech.edu/~ genmark |
|
|
|
|
genmark@ford.gatech.edu |
|
|
GENVIEW |
Milanesi et al., 1993 |
www.itba.mi.cnr.it/webgene |
|
|
GREAT |
Gelfand and Roytberg, 1993 |
|
|
|
GRAIL II / GAP |
Xu et al., 1994 |
avalon.epm.ornl.gov/gallery.html |
|
|
|
|
grail@ornl.gov |
|
|
FGENEH |
Solovyev et al., 1994 |
dot.imgen.bcm.tmc.edu:9331/gene-finder/gf.html |
|
|
|
|
service@bchs.uh.edu |
|
|
GENELANG |
Dong and Searls, 1994 |
cbil.humgen.upenn.edu/~ sdong/genlang_home.html |
|
|
|
|
genlang@cbil.humgen.upenn.edu |
|
|
XPOUND |
Thomas and Skolnick, 1994 |
|
|
|
GENIE |
Kulp et al., 1996 |
www-hgc.lbl.gov/inf/genie.html |
|
|
PROCRUSTES |
Gelfand et al., 1996 |
www-hto.usc.edu/software/procrustes/ |
|
|
MZEF |
Zhang, 1997 |
www.cshl.org/genefinder |
|
|
GENSCAN |
Burge and Karlin, 1997 |
gnomic.stanford.edu/GENSCANW.html |
|
|
MORGAN |
Salzberg et al., 1997 |
www.cs.jhu.edu/labs/compbio/morgan.html |
|
|
VEIL |
Henderson et al., 1997 |
www.cs.jhu.edu/labs/compbio/veil.html |
|
|
A general strategy among gene identification programs is to integrate
the output of a number of coding statistics. Thus,
to name just a few examples, the popular Grail program
[Uberbacher and Mural1991] uses
a neural network to integrate a number of coding statistics,
mostly related to Hexamer Usage and Position Asymmetry in base composition.
Solovyev et al. solovyev:1994a in the Fgeneh program use
linear discriminant analysis,
while Dong and Searls dong:1994a in GenLang use linguistic methods.
Although increased accuracy in the gene predictions is obtained in this
way, because coding statistics are all
essentially measuring codon usage bias in one way or another, their
output is strongly correlated [Fickett and Tung1992].
Indeed, Table 6 shows the correlation between the
scores of the coding statistics reviewed here in the set of human exon
and intron sequences. As it can be seen, the coding statistics are
strongly correlated. The only two statistics truly uncorrelated
are Codon Preference and Amino Acid Usage in exonic sequences,
as otherwise expected.
It appears, thus, that some combination of just two statistics, one measuring
correlation between positions within a codon, and the other measuring
dependence between codons along the query sequence could produce the most
discriminant output.
Table:
Correlation between the different coding statistics in
our set of exonic (upper triangle of the table) and intronic
(lower triangle) sequences. The scores of the model dependent coding statistics
and of the Fourier Spectrum have been divided by the length of the sequence
to compute the correlations. (Abbreviations:
CU Codon Usage,
HU Hexamer Usage,
CPre Codon Preference,
AAU Amino Acid Usage,
CPro Codon Prototype,
MM-1 Markov Model k=1,
MM-2 Markov Model k=2,
MM-3 Markov Model k=3,
PA Position Assymetry,
PAI Periodic Assymetry Index,
AMI Average Mutual Information,
FOU Fourier Spectrum)
|
|
CU |
HU |
CPre |
AAU |
CPro |
MM-1 |
MM-2 |
MM-5 |
PA |
PAI |
AMI |
FOU |
|
Codon Usage |
|
0.908 |
0.769 |
0.492 |
0.803 |
0.876 |
0.909 |
0.772 |
0.590 |
0.558 |
0.529 |
0.562 |
|
Hexamer Usage |
0.925 |
|
0.822 |
0.287 |
0.802 |
0.912 |
0.928 |
0.869 |
0.585 |
0.544 |
0.510 |
0.559 |
|
Codon Preference |
0.927 |
0.932 |
|
-0.069 |
0.637 |
0.833 |
0.838 |
0.723 |
0.456 |
0.415 |
0.421 |
0.438 |
|
Amino Acid Usage |
0.738 |
0.626 |
0.537 |
|
0.351 |
0.238 |
0.262 |
0.199 |
0.392 |
0.391 |
0.355 |
0.383 |
|
Codon Prototype |
0.822 |
0.820 |
0.782 |
0.623 |
|
0.810 |
0.799 |
0.673 |
0.708 |
0.659 |
0.611 |
0.662 |
|
Markov Model, k=1 |
0.943 |
0.941 |
0.952 |
0.604 |
0.875 |
|
0.969 |
0.801 |
0.543 |
0.502 |
0.465 |
0.512 |
|
Markov Model, k=2 |
0.974 |
0.944 |
0.952 |
0.665 |
0.853 |
0.976 |
|
0.831 |
0.535 |
0.494 |
0.459 |
0.507 |
|
Markov Model, k=5 |
0.919 |
0.932 |
0.913 |
0.621 |
0.816 |
0.928 |
0.950 |
|
0.465 |
0.428 |
0.400 |
0.435 |
|
Position Assymetry |
0.326 |
0.381 |
0.318 |
0.355 |
0.392 |
0.321 |
0.320 |
0.344 |
|
0.953 |
0.937 |
0.979 |
|
Periodic Assymetry Index |
0.299 |
0.363 |
0.283 |
0.369 |
0.266 |
0.256 |
0.276 |
0.292 |
0.531 |
|
0.924 |
0.912 |
|
Average Mutual Information |
0.225 |
0.267 |
0.216 |
0.247 |
0.314 |
0.217 |
0.228 |
0.251 |
0.873 |
0.469 |
|
0.911 |
|
Fourier Spectrum |
0.381 |
0.455 |
0.373 |
0.432 |
0.414 |
0.363 |
0.370 |
0.401 |
0.914 |
0.713 |
0.726 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Borodovsky and McIninch1993
-
BORODOVSKY, M. AND MCININCH, J. 1993.
Genmark: Parallel gene recognition for both dna strands.
Computer and Chemistry 17:123-13.
- Burge and Karlin1997
-
BURGE, C. AND KARLIN, S. 1997.
Prediction of complete gene structures in human genomic dna.
Journal of Molecular Biology 268:78-94.
- Burset and Guigó1996
-
BURSET, M. AND GUIGÓ, R. 1996.
Evaluation of gene structure prediction programs.
Genomics 34:353-357.
- Claverie1997
-
CLAVERIE, J. M. 1997.
Computational methods for the identification of genes in vertebrate
genomic sequences.
Human Molecular Genetics 6:1735-1744.
- Claverie et al.1990
-
CLAVERIE, J.-M., SAUVAGET, I., AND BOUGUELERET, L. 1990.
k-tuple frequency analysis: From intron/exon discrimination to t-cell
epitope mapping.
Methods in Enzymology 183:237-252.
- Dong and Searls1994
-
DONG, S. AND SEARLS, D. B. 1994.
Gene structure prediction by linguistic methods.
Genomics 23:540-551.
- Fichant and Gautier1987
-
FICHANT, G. AND GAUTIER, C. 1987.
Statistical method for predicting coding regions in nucleic acid
sequences.
Nucleic Acids Research 4:287-295.
- Fickett1982
-
FICKETT, J. W. 1982.
Recognition of protein coding regions in dna sequences.
Nucleic Acids Research 10:5303-5318.
- Fickett1996
-
FICKETT, J. W. 1996.
Finding genes by computer: the state of the art.
Trends in Genetics 12:316-320.
- Fickett and Tung1992
-
FICKETT, J. W. AND TUNG, C. S. 1992.
Assessment of protein coding measures.
Nucleic Acids Research 20:6441-6450.
- Gelfand1995
-
GELFAND, M. S. 1995.
Prediction of function in dna sequence analysis.
Journal of Computational Biology 1:87-115.
- Grantham et al.1980
-
GRANTHAM, R., GAUTIER, C., GOUY, M., MERCIER, R., AND PAVE, A. 1980.
Codon catalog usage and the genome hypothesis.
Nucleic Acids Research 8:49-62.
- Gribskov et al.1984
-
GRIBSKOV, M., DEVEREUX, J., AND BURGESS, R. B. 1984.
The codon preference plot: graphic analysis of protein coding
sequences and prediction of gene expression.
Nucleic Acids Research 12:539-549.
- Gro
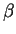 e et al.1998
e et al.1998
-
GROE, I., HERZEL, H., BULDYREV, S. V., AND STANLEY, H. E. 1998.
A species-independent measure for distinguishing coding and noncoding
dna.
submitted .
- Guigó1997a
-
GUIGÓ, R. 1997a.
Computational gene identification.
Journal of Molecular Medicine 75:389-393.
- Guigó1997b
-
GUIGÓ, R. 1997b.
Computational gene identification: An open problem.
Computers and Chemistry 21:215-222.
- Gutiérrez et al.1994
-
GUTIÉRREZ, G., OLIVER, J., AND MARÍN, A. 1994.
On the origin of the periodicity of three in protein coding dna
sequences.
Journal of theoretical Biology 167:413-414.
- Henderson et al.1997
-
HENDERSON, J., SALZBERG, S., AND FASSMAN, K. H. 1997.
Finding genes in dna with a hidden markov model.
Journal of Computational Biology 4:127-141.
- Herzel and Gro
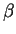 e1995
e1995
-
HERZEL, H. AND GROE, I. 1995.
Measuring correlations in symbol sequences.
Physica A 216:518-542.
- Ikemura1985
-
IKEMURA, T. 1985.
Codon usage and trna content in unicellular and multicellular
organisms.
Molecular Biology and Evolution 2:13-34.
- Konopka1994
-
KONOPKA, A. K. 1994.
Structure and Methods: VI. Human Genome Initiative and DNA
Recombination, chapter Towards Mapping Functional Domains in Indiscriminantly
Sequenced Nucleic Acids: A Computational Approach.
Adenine Press, Guilderland, New York.
- Kulp et al.1996
-
KULP, D., HAUSSLER, D., REESE, M., AND EECKMAN, F. H. 1996.
A generalized hidden markov model for the recognition of human genes
in dna.
In D. J. States, P. Agarwal, T. Gaasterland, L. Hunter, and R.
Smith (eds.), Intelligent Systems for Molecular Biology, pp. 134-142, Menlo
Park, California. AAAI press.
- Li1997
-
LI, W. 1997.
The study of correlation structures of dna sequences: a critical
review.
Computer and Chemistry 21:257-271.
- Li et al.1994
-
LI, W., MARR, T. G., AND KANEKO, K. 1994.
Understanding long-range correlations in dna sequences.
Physica D 75:392-416.
- McCaldon and Argos1988
-
MCCALDON, P. AND ARGOS, P. 1988.
Proteins: Structure, Function and Genetics 4:99-122.
- Mural et al.1991
-
MURAL, R. J., MANN, R. C., AND UBERBACHER, E. C. 1991.
In C. C. Cantor and H. A. Lim (eds.), Proceedings of the First
International Conference on Electrophoresis, Supercomputing and the Human
Genome, pp. 164-172. World Scientific Co.
- Shannon1948
-
SHANNON, C. E. 1948.
A mathematical theory of communication.
Bell Syst. The Bell System Technical Journal 27:379-423.
- Shepherd1981
-
SHEPHERD, J. C. 1981.
Method to determine the reading frame of a protein from the
purine/pyrimidine genome sequence and its possible evolutionary
justification.
Proceedings National Academy Sciences USA. 78:1596-1600.
- Silverman and Linsker1986
-
SILVERMAN, B. D. AND LINSKER, R. 1986.
A measure of dna periodicity.
Journal of theoretical Biology 118:295-300.
- Solovyev et al.1994
-
SOLOVYEV, V. V., SALAMOV, A. A., AND LAWRENCE, C. B. 1994.
Predicting internal exons by oligonucleotide composition and
discriminant analysis of spliceable open reading frames.
Nucleic Acids Research 22:5156-5163.
- Staden1984
-
STADEN, R. 1984.
Measurements of the effects that coding for a protein has on a dna
sequence and their use for finding genes.
Nucleic Acids Research 12:551-567.
- Staden and McLachlan1982
-
STADEN, R. AND MCLACHLAN, A. 1982.
Codon preference and its use in identifying protein coding regions in
long dna sequences.
Nucleic Acids Research 10:141-156.
- Tiwari et al.1997
-
TIWARI, S., RAMACHANDRAN, S., BHATTACHARYA, A., BHATTACHARYA, S., AND
RAMASWAMY, R. 1997.
Prediction of probable genes by fourier analysis of genomic
sequences.
Computer Applications in the Biosciences 13:263-270.
- Tsonis et al.1991
-
TSONIS, A. A., ELSNER, J. B., AND TSONIS, P. A. 1991.
Periodicity in dna coding sequences: implications in gene evolution.
Journal of Theoretical Biology 151:323.
- Uberbacher and Mural1991
-
UBERBACHER, E. C. AND MURAL, R. J. 1991.
Locating protein-coding regions in human dna sequences by a multiple
sensor-neural network approach.
Proceedings National Academy Sciences USA 88:11261-11265.
DNA Composition, Codon Usage and Exon Prediction
This document was generated using the
LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 1 -show_section_numbers main
The translation was initiated by Roderic Guigo Serra on 2000-02-07



Roderic Guigo Serra
2000-02-07
![]() -globin gene. The sequence has been
extracted from the GenBank entry HUMHBB (EMBL entry HSHBB),
from positions 62,001 to 64,000. The human
-globin gene. The sequence has been
extracted from the GenBank entry HUMHBB (EMBL entry HSHBB),
from positions 62,001 to 64,000. The human ![]() -globin gene has three
coding exons in positions 187-278, 409-631, and 1482-1610,
relative to the 2000 bp test sequence. In addition, we have
extracted two subsequences from this test sequence. The complete sequence
of the second coding exon of the
-globin gene has three
coding exons in positions 187-278, 409-631, and 1482-1610,
relative to the 2000 bp test sequence. In addition, we have
extracted two subsequences from this test sequence. The complete sequence
of the second coding exon of the ![]() -globin gene,
which is 223 bp long, and a 223 bp long sequence
from the middle of the second intron (from positions 800 to 1022 of the
test sequence). These two sequences will serve as exonic and intronic test
sequences. We have also extracted from GenBank rel. 93 (February 1996),
a set of 450 human genes following the protocol described
in Burset and Guigó burset:1996a (see also Guigó
guigo:1997b).
From this set, exons longer than 100bp
and introns longer than 100 bp and shorter than 2500 bp were kept.
This resulted in 1753 introns and 1761 exons.
The distribution of the scores of the different coding statistics analyzed
here will be plotted in these two sets of sequences.
Results obtained in the exonic, intronic and genomic
test sequences are only for illustration purposes, and differences in
the performance of different coding statistics can not be inferred from them.
Readers interested in a rigorous comparative benchmarking should refer to
Fickett and Tung fickett:1992a.
-globin gene,
which is 223 bp long, and a 223 bp long sequence
from the middle of the second intron (from positions 800 to 1022 of the
test sequence). These two sequences will serve as exonic and intronic test
sequences. We have also extracted from GenBank rel. 93 (February 1996),
a set of 450 human genes following the protocol described
in Burset and Guigó burset:1996a (see also Guigó
guigo:1997b).
From this set, exons longer than 100bp
and introns longer than 100 bp and shorter than 2500 bp were kept.
This resulted in 1753 introns and 1761 exons.
The distribution of the scores of the different coding statistics analyzed
here will be plotted in these two sets of sequences.
Results obtained in the exonic, intronic and genomic
test sequences are only for illustration purposes, and differences in
the performance of different coding statistics can not be inferred from them.
Readers interested in a rigorous comparative benchmarking should refer to
Fickett and Tung fickett:1992a.
![]() is a sequence
of codons
is a sequence
of codons
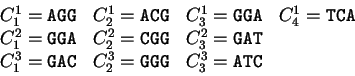
![]() is a codon, we will use
is a codon, we will use ![]() to denote the
nucleotide occupying position
to denote the
nucleotide occupying position ![]() in the codon. For instance, in
the example above
in the codon. For instance, in
the example above
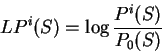
![]() in the three different frames,
and plotting the highest value obtained. In this case, the resulting
profile reproduces fairly well the exonic structure of the human
in the three different frames,
and plotting the highest value obtained. In this case, the resulting
profile reproduces fairly well the exonic structure of the human
![]() -globin gene.
-globin gene.
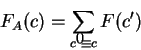
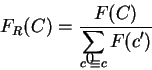
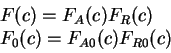
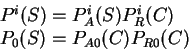

![]() be the probability of nucleotide
be the probability of nucleotide ![]() at codon position
at codon position ![]() , as
estimated from known coding regions (Table 2). Then,
if
, as
estimated from known coding regions (Table 2). Then,
if ![]() is a codon
is a codon
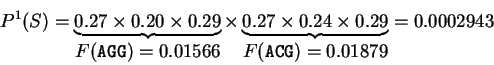
![]() matrices (the transition matrices) are required,
matrices (the transition matrices) are required,
![]() ,
, ![]() , and
, and ![]() , each one corresponding to a different codon position.
Coefficient
, each one corresponding to a different codon position.
Coefficient ![]() from matrix
from matrix ![]() ,
, ![]() ,
corresponds to the probability of
nucleotide
,
corresponds to the probability of
nucleotide ![]() in codon position
in codon position ![]() (position
(position ![]() , if
, if ![]() ), given that
nucleotide
), given that
nucleotide ![]() is at codon position
is at codon position ![]() . We have estimated these matrices
from the sample of 1761 human exons.
The conditional probability of nucleotides
. We have estimated these matrices
from the sample of 1761 human exons.
The conditional probability of nucleotides
![]() in codon position
in codon position ![]() , given nucleotide
, given nucleotide ![]() in codon position
in codon position ![]() ,
is estimated by the number of times that
di-nucleotide
,
is estimated by the number of times that
di-nucleotide ![]() appears at codon position
appears at codon position ![]() over the total number of times that
nucleotide
over the total number of times that
nucleotide ![]() appears at codon position
appears at codon position ![]() .
These matrices are shown in Table 3.
Indeed, we can see from them that
the probability of G at codon position 3, given that C is
at codon position 2, is 0.27, but the probability of G at codon
position 3 given that G is at codon position 2 is 0.37.
.
These matrices are shown in Table 3.
Indeed, we can see from them that
the probability of G at codon position 3, given that C is
at codon position 2, is 0.27, but the probability of G at codon
position 3 given that G is at codon position 2 is 0.37.
![]() above, given that
above, given that ![]() is coding in frame 1,
can be computed now as
is coding in frame 1,
can be computed now as
![]() , given that
, given that
![]() codes in frame 2 is
codes in frame 2 is
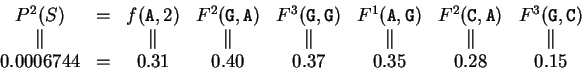
![]() , for instance, would be the probability of A
following the di-nucleotide GC at codon position 2 (that is, A
would be at codon position 1).
In general, the order of the Markov Model indicates the number of
preceding nucleotides on which the probability of a given nucleotide depends.
In a Markov Model of order
, for instance, would be the probability of A
following the di-nucleotide GC at codon position 2 (that is, A
would be at codon position 1).
In general, the order of the Markov Model indicates the number of
preceding nucleotides on which the probability of a given nucleotide depends.
In a Markov Model of order ![]() , thus, the coefficients
, thus, the coefficients ![]() correspond to the probability of oligonucleotide
correspond to the probability of oligonucleotide ![]() of length
of length ![]() at codon position
at codon position ![]() , given oligonucleotide
, given oligonucleotide ![]() of length
of length ![]() at codon
position
at codon
position ![]() . These probabilities are estimated by the frequency of
oligonucleotide
. These probabilities are estimated by the frequency of
oligonucleotide ![]() of length
of length ![]() at codon position
at codon position ![]() over the frequency of oligonucleotide
over the frequency of oligonucleotide ![]() of length
of length
![]() at position
at position ![]() .
Borodovsky and McIninch borodovsky:1993a investigate Markov Models
of order up to
.
Borodovsky and McIninch borodovsky:1993a investigate Markov Models
of order up to ![]() .
Results obtained in the test sequences with
Markov Models of order 2 and 5 are shown in
Table 4, and Figures 1 and
2.
.
Results obtained in the test sequences with
Markov Models of order 2 and 5 are shown in
Table 4, and Figures 1 and
2.
![]() matrices (corresponding
to the three transition matrices and the initial probabilities matrix),
that is, it depends on 256 estimated probabilities.
A similar reasoning can be applied to the relationships between Hexamer
Usage and Markov Models of order
matrices (corresponding
to the three transition matrices and the initial probabilities matrix),
that is, it depends on 256 estimated probabilities.
A similar reasoning can be applied to the relationships between Hexamer
Usage and Markov Models of order ![]() .
.
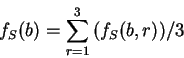
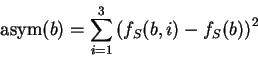
![]() (that
is, at the same codon position) in the
query sequence with the probability of these pairs to appear at other
distances (different codon positions),
Herzel and Große herzel:1995a in the Average Mutual Information,
compare the correlations of all pairs of
nucleotides at the same codon positions with the correlations
at different codon positions. Finally, Tiwari et al.
tiwari:1997a use the relative
peak at the frequency
(that
is, at the same codon position) in the
query sequence with the probability of these pairs to appear at other
distances (different codon positions),
Herzel and Große herzel:1995a in the Average Mutual Information,
compare the correlations of all pairs of
nucleotides at the same codon positions with the correlations
at different codon positions. Finally, Tiwari et al.
tiwari:1997a use the relative
peak at the frequency ![]() in the Fourier spectrum of the sequence.
in the Fourier spectrum of the sequence.

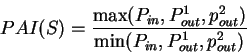
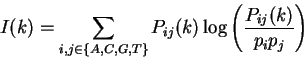
![]() oscillates between two values, while
in non-coding DNA,
oscillates between two values, while
in non-coding DNA, ![]() is rather flat.
Herzel and Große herzel:1995a use this fact to construct a
coding statistic.
They call the two values between which
is rather flat.
Herzel and Große herzel:1995a use this fact to construct a
coding statistic.
They call the two values between which ![]() oscillates in coding DNA,
the in-frame mutual information
oscillates in coding DNA,
the in-frame mutual information ![]() at distances
at distances
![]() , and the out-of-frame mutual information
, and the out-of-frame mutual information
![]() at
at
![]() .
They show that
.
They show that
![]() and
and ![]() can be computed directly from the probabilities
can be computed directly from the probabilities
![]() of the nucleotide
of the nucleotide ![]() to appear at codon position
to appear at codon position
![]() , as estimated from
, as estimated from ![]() . In order to reduce the pair of numbers
. In order to reduce the pair of numbers
![]() and
and ![]() to a single quantity, they compute the
Average Mutual Information as [Gro
to a single quantity, they compute the
Average Mutual Information as [Gro![]() e et al.1998]
e et al.1998]

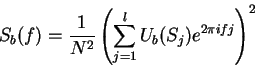
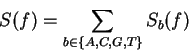
![]() over the average of the total spectrum of the sequence,
over the average of the total spectrum of the sequence,
![]() ,
which can be computed from the frequencies of the nucleotides along
the sequence.
,
which can be computed from the frequencies of the nucleotides along
the sequence.